
经过漫长的等待后,果然头条的面试挂掉了。突然发现自己打了这么久的ACM,很多基础数据结构的概念掌握的还不是非常的牢固。这些数据结构可能并不难,特别是跳表和线段数组这样的数据结构,但是由于平日的疏忽导致这些概念有少许的以往。那么今天就要对这些掌握不是特别牢固的数据结构一一进行总结。
一 跳表
跳表是一个随机化的数据结构,实质就是一种可以进行二分查找的有序链表。
跳表在原有的有序链表上面增加了多级索引,通过索引来实现快速查找。
跳表不仅能提高搜索性能,同时也可以提高插入和删除操作的性能。
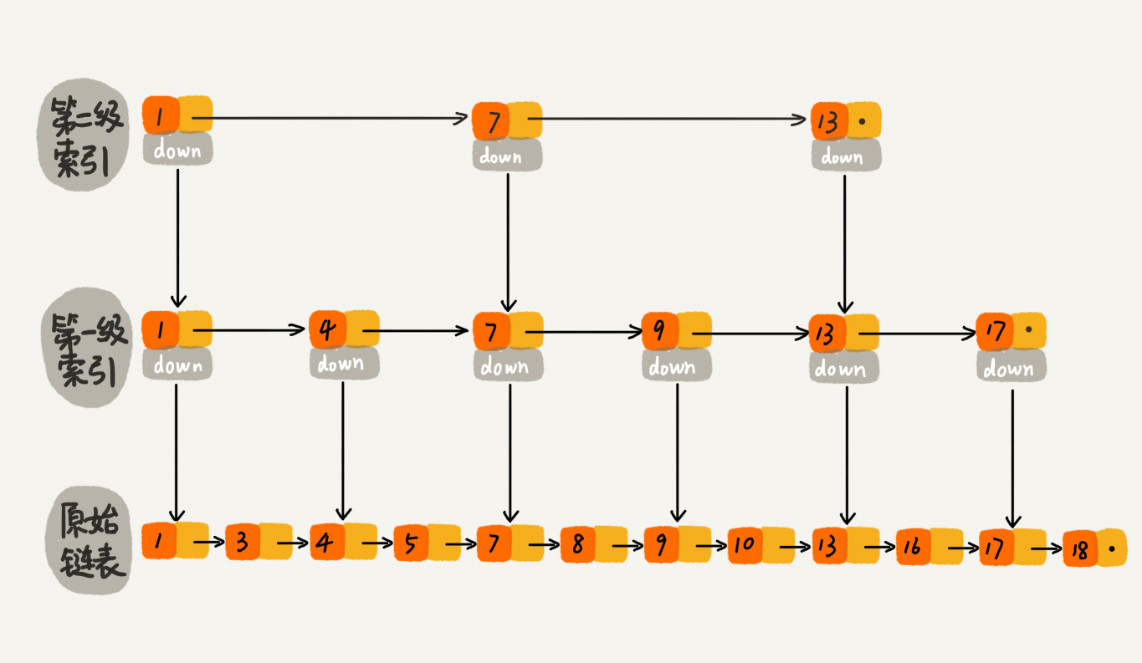
假设每M个元素构建索引,元素链表中总共有N个元素,那么构建的索引数如下:
第一级有:n/M 个
第二级有:n/(M^2)个元素
…….
第k级有:n/(M^k)个元素
假设第k级为最后一级则可知,n/(M^k) = M, k = logn - 1, 再加上原始链表总共logn级平均每级搜索元素个数 = M + 1 ;
时间复杂度 = O(log(n))
空间复杂度 = n/M + n/(M^2) + … + n/(M^k) = O(n)
引用自简书liuzhengqiu
二 线段树
了解线段树前我们需要了解二叉树,线段树是二叉树的一种,他是一颗二叉搜索树。线段树上的每一个节点代表一个区间,同样也可以理解为一个线段,搜索则是在这些线段上进行搜索从而获得答案。
为了进一步的学习线段树,我们首先需要了解线段树的功能是什么,有过OI基础/ACM基础的同学们通常会认为线段树主要用于处理区间查询问题。但是在实际应用中可能线段树的功能比区间查询更加丰富,当然这里我们还是需要从区间查询问题开始说起。
更新点,查询区间
更新区间,查询点
更新区间,查询区间
通常来说,利用线段树处理的问题分为上面三种,通常而言线段树的时间复杂度是O(log2(N)),线段树的空间复杂度<4n。下面通过一张图来显示线段树每个节点储存的信息,例子采用的是区间长度为10的数组。
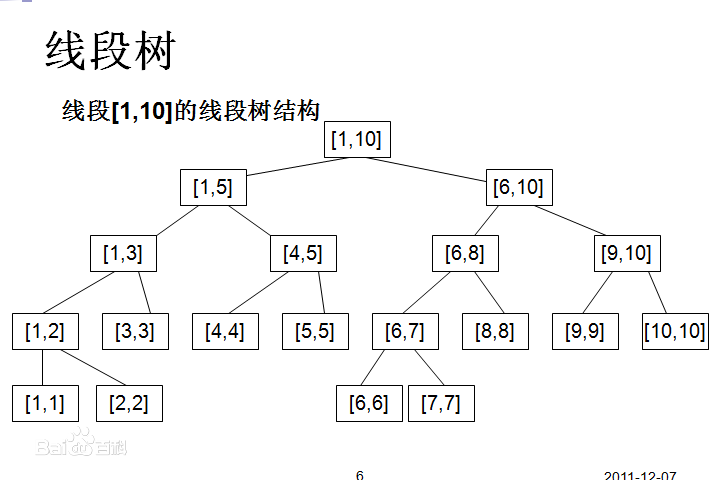
可以发现,每个叶子结点的值就是数组的值,每个非叶子结点的度都为二,且左右两个孩子分别存储父亲一半的区间。每个父亲的存储的值也就是两个孩子存储的值的最大值。
通过对上图的观察我们现在可以清晰的了解线段树点更新,区间更新,点查询,区间查询的方法。具体的代码需要在网上寻找,每个人都有自己独特的写法,如果是竞赛选手,强烈建议形成自己的一套模板。
三 线段数组
要了解线段数组,我们需要先了解树状数组,顾名思义,树状数组即利用数组构建树形结构。这种结构相比树形结构可以极大程度的降低内存的消耗,故在比赛中我们常常利用树状数组来解决线段树的问题,而不是动态开点。
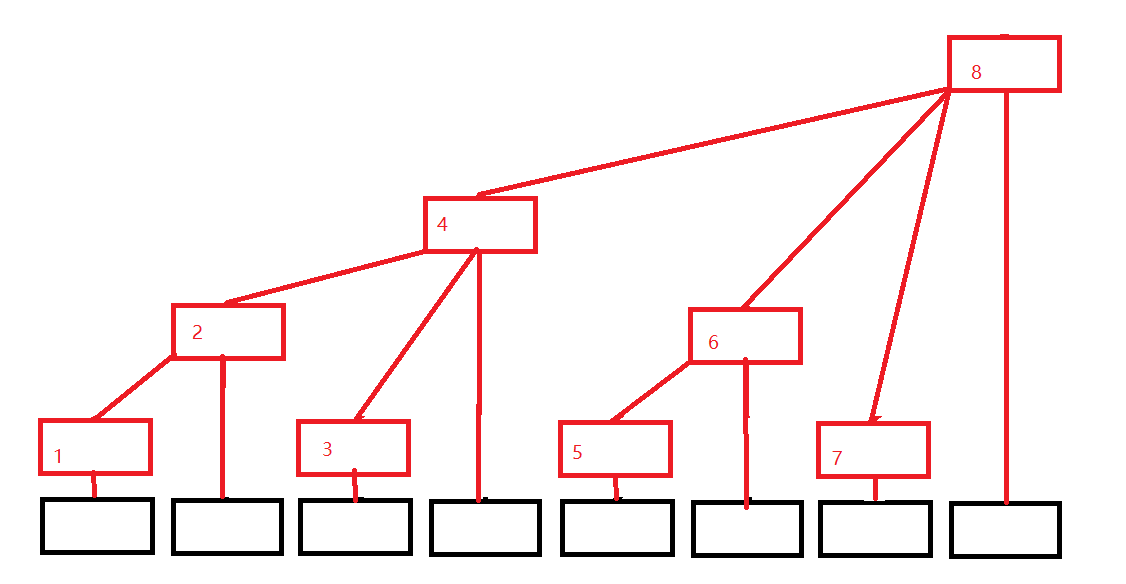
与普通的线段树相同,利用线段数组可以轻松的完成区间的修改、查询。他的复杂度和线段树相同均为O(logN),但是相比线段树,树状数组拥有更小的常数,所以最终运行的速度更快。
四 红黑树
红黑树具有下面五种特征:
性质1:每个节点要么是黑色,要么是红色。
性质2:根节点是黑色。
性质3:每个叶子节点(NIL)是黑色。
性质4:每个红色结点的两个子结点一定都是黑色。
性质5:任意一结点到每个叶子结点的路径都包含数量相同的黑结点。
红黑树是一种特殊的二叉平衡树,它通过左旋,右旋和变色来保持自平衡。他是一个非常负责的数据结构,在本篇中仅简单介绍其功能。更加丰富的内容日后会开专题介绍。